Non-minimum phase case

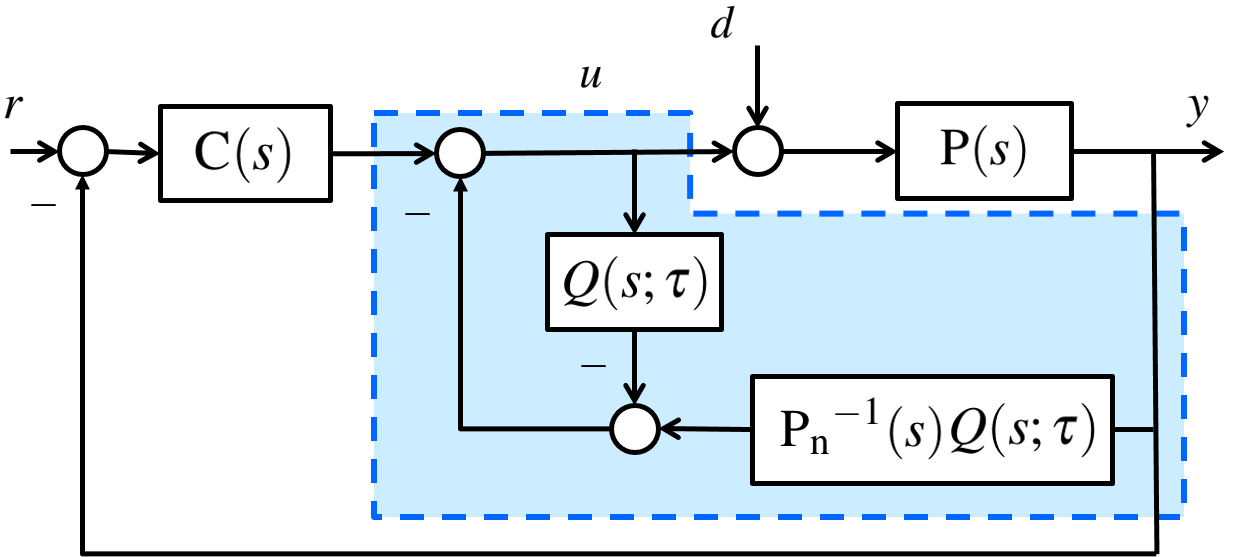
It is assumed that in the figure,

• ,
• ,
• , where ,
• .

Setup

---

The following code returns a structure variable sysEnv that contains the information about the system environment that will be used later in designing the DOB.

C = tf(1, [1, 1]);
P_n = tf([1, 1, 5], [1, 3, 3, 1]);

N = {1, [-0.2, 2], 5};
D = {1, 3, 3, 1};

sysEnv = setup_sys(N, D, P_n, C)

The field nominalStab is 1 since the nominal closed-loop system is stable, but the field minPhase is 0 since a given set of uncertain plants contains some non-minimum phase systems. Therefore, there exists a constant such that, for all , the closed-loop system is not robustly stable.

Design of Q-filter

---

Then let’s see if the closed-loop system is robustly stable for a particular (sufficiently large) . First of all, the following code informs you that the fast dynamics of the closed-loop system is robustly stable.

Qcanon = tf(1, [1, 1]);
isFastDynamicsStable(sysEnv, Qcanon)

After several trials and errors like the following code (Unfortunately, you should read the paper to understand the systematic way!), you can find out that at least robustly stabilizes the closed-loop system.

isValidTau(sysEnv, Qcanon, 0.18)
isValidTau(sysEnv, Qcanon, 0.19)
isValidTau(sysEnv, Qcanon, 0.20)
isValidTau(sysEnv, Qcanon, 0.21)

In conclusion, DO-DAT suggests you to use the Q-filter for the robust stability of the closed-loop system as follows. Although this result does not guarantee any level of performance in terms of disturbance rejection, you can notice that DOB is still available for non-minimum phase plant.

, for .